Source (restricted to non-HBO-Max regions)
Kamala Harris is known to love Venn diagrams and would be cringing hard at this.
For reference, circles in Venn (Euler) diagrams are sets of objects with a certain property. Select objects are shown inside or outside of each circle depending on whether they belong to the set.
A good example is xkcd 2962:
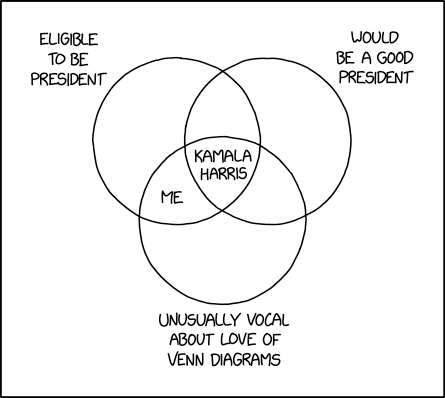


It’s certainly not very useful or informative.
But please explain how it is incorrect.
In a Venn diagram, the overlap is what the individual areas have in common. It’s the intersection, not the union.
Well for starters Kamabla is not actually at the intersection of Kama and Bla…
You have two strings and in the overlap you have the concatenated string formed from the parts. Again, not useful but a totally valid interpretation.
So … can you actually explain why you think it is incorrect or is snarky comments all you got?
This article on Intersection might help you understand
Here are the basics, though:
That picture does not make it clear that the labels refer to regions, not elements. A clearer explanation of set operators is the following:
What relation function matches your interpretation?
Since you’re the Venn diagram expert now…