cross-posted from: https://lemmy.world/post/19541930
Preferably a Holocene colander?
A consensus view was formally adopted by the IUGS in 2013, placing its start at 11,700 years before 2000 (9701 BC), about 300 years more recent than the epoch of the Holocene calendar.[6]
Some problems with Gregorian calendar
The Gregorian calendar improves the approximation made by the Julian calendar by skipping three Julian leap days in every 400 years, giving an average year of 365.2425 mean solar days long.[82] This approximation has an error of about one day per 3,030 years[s] with respect to the current value of the mean tropical year. However, because of the precession of the equinoxes, which is not constant, and the movement of the perihelion (which affects the Earth’s orbital speed) the error with respect to the astronomical vernal equinox is variable; using the average interval between vernal equinoxes near 2000 of 365.24237 days[83] implies an error closer to 1 day every 7,700 years. By any criterion, the Gregorian calendar is substantially more accurate than the 1 day in 128 years error of the Julian calendar (average year 365.25 days).
In the 19th century, Sir John Herschel proposed a modification to the Gregorian calendar with 969 leap days every 4,000 years, instead of 970 leap days that the Gregorian calendar would insert over the same period.[84] This would reduce the average year to 365.24225 days. Herschel’s proposal would make the year 4000, and multiples thereof, common instead of leap. While this modification has often been proposed since, it has never been officially adopted.[85]
On time scales of thousands of years, the Gregorian calendar falls behind the astronomical seasons. This is because the Earth’s speed of rotation is gradually slowing down, which makes each day slightly longer over time (see tidal acceleration and leap second) while the year maintains a more uniform duration.
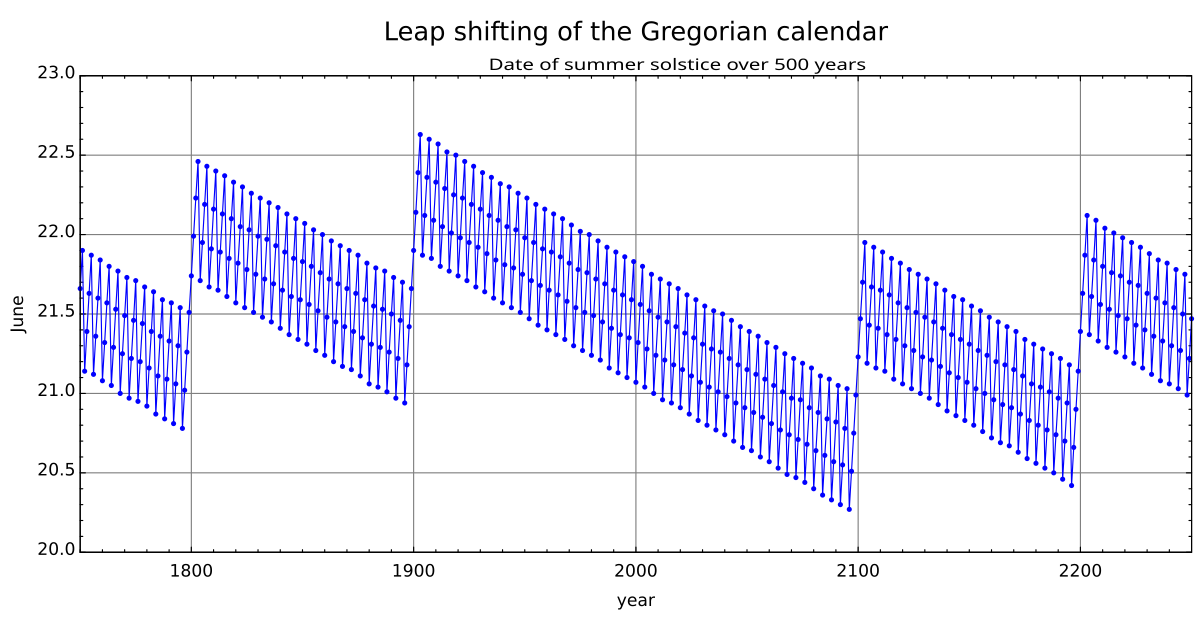
Calendar seasonal error Gregorian calendar seasons difference
This image shows the difference between the Gregorian calendar and the astronomical seasons.
The y-axis is the date in June and the x-axis is Gregorian calendar years.
Each point is the date and time of the June solstice in that particular year. The error shifts by about a quarter of a day per year. Centurial years are ordinary years, unless they are divisible by 400, in which case they are leap years. This causes a correction in the years 1700, 1800, 1900, 2100, 2200, and 2300.
For instance, these corrections cause 23 December 1903 to be the latest December solstice, and 20 December 2096 to be the earliest solstice—about 2.35 days of variation compared with the astronomical event.
Proposed reforms The following are proposed reforms of the Gregorian calendar:
Holocene calendar
International Fixed Calendar (also called the International Perpetual calendar)
World Calendar
World Season Calendar
Leap week calendars
Pax Calendar
Symmetry454
Hanke–Henry Permanent Calendar


Instead of trying to synchronize the year with the solstices, which vary unpredictably over time, just have every planet’s year start when it passes between its sun and the center of the galaxy. That will depend only on the orbit’s period, which is more consistent over time.
Not all planets pass directly between their star and the centre of the galaxy. The plane of our own solar system isn’t lined up with the plane of the galaxy, for example. If the Sun were attached to Sagittarius A* by a thin cotton thread, I’m pretty sure none of the planets would hit it.
We’d perhaps have to define it as the centre of the planet crossing the unique plane that both passes through the star and the centre of the galaxy and is perpendicular to the planet’s orbit relative to the star. And for some planets in some systems that would still be hard to calculate on account of an extremely oblique crossing angle.
And even then there might be severe problems with that for systems closer to the galactic core that are stable, but otherwise weirdly affected by nearby gravitational effects.
Also, what about planets that are far enough out to orbit two stars? Do we switch to barycentres and which do we use?
And what about moon dwellers or binary planetary systems? Pluto and Charon orbit a point that is outside both. There are further complications there.
I’d rather define it as the point where a ray from the star through the planet crosses the pole passing through the galactic center perpendicular to the plane of the galaxy. Make it depend as little as possible on the planet’s orbital characteristics. (And yeah—use barycenters for binary stars and planets.)
That’ll be a problem for that one system that’s at right angles to the plane of the galaxy, but I suppose it could work otherwise.
I can also envisage situations where systems that are close to being at right angles to the galactic plane have the different star-planet lines cross the galactic polar line at opposite sides of the star due to slight variances in relative orbital plane. None of our planets are exactly aligned that way, for example.
Perhaps that’s not a concern though.
Given the dynamic nature of planetary orbits and the motion of stars around the galaxy, edge cases likely won’t stay edge cases for long—so predict ahead to see how the case will eventually resolve itself, and use that solution preemptively.