What concepts or facts do you know from math that is mind blowing, awesome, or simply fascinating?
Here are some I would like to share:
- Gödel’s incompleteness theorems: There are some problems in math so difficult that it can never be solved no matter how much time you put into it.
- Halting problem: It is impossible to write a program that can figure out whether or not any input program loops forever or finishes running. (Undecidablity)
The Busy Beaver function
Now this is the mind blowing one. What is the largest non-infinite number you know? Graham’s Number? TREE(3)? TREE(TREE(3))? This one will beat it easily.
- The Busy Beaver function produces the fastest growing number that is theoretically possible. These numbers are so large we don’t even know if you can compute the function to get the value even with an infinitely powerful PC.
- In fact, just the mere act of being able to compute the value would mean solving the hardest problems in mathematics.
- Σ(1) = 1
- Σ(4) = 13
- Σ(6) > 101010101010101010101010101010 (10s are stacked on each other)
- Σ(17) > Graham’s Number
- Σ(27) If you can compute this function the Goldbach conjecture is false.
- Σ(744) If you can compute this function the Riemann hypothesis is false.
Sources:
- YouTube - The Busy Beaver function by Mutual Information
- YouTube - Gödel’s incompleteness Theorem by Veritasium
- YouTube - Halting Problem by Computerphile
- YouTube - Graham’s Number by Numberphile
- YouTube - TREE(3) by Numberphile
- Wikipedia - Gödel’s incompleteness theorems
- Wikipedia - Halting Problem
- Wikipedia - Busy Beaver
- Wikipedia - Riemann hypothesis
- Wikipedia - Goldbach’s conjecture
- Wikipedia - Millennium Prize Problems - $1,000,000 Reward for a solution


I think the four small countries inside would each only have 2 neighbours. So you could take 2 that are diagonal and make them the same colour.
Looks to be that way one of the examples given on the wiki page. It is still however an interesting theory, if four countries touching at a corner, are the diagonal countries neighbouring each other or not. It honestly feels like a question that will start a war somewhere at sometime, probably already has.
In graph theory there are vertices and edges, two shapes are adjacent if and only if they share an edge, vertices are not relevant to adjacency. As long as all countries subscribe to graph theory we should be safe
The only problem with that it that it requires all countries to agree to something, and that seems to become harder and harder nowadays.
Someone beat me to it, so I thought I’d also include the adjacency graph for the countries, it can be easier to see the solution to colouring them.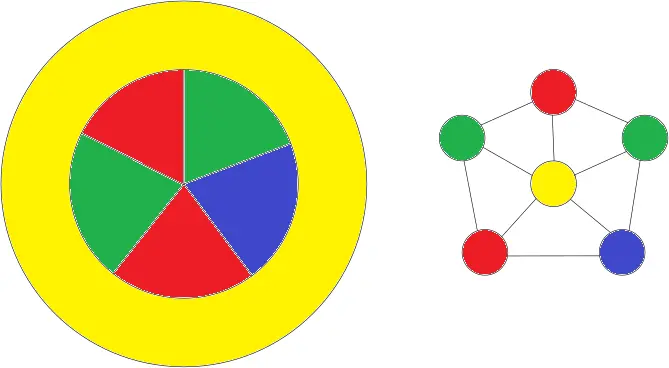
But each small country has three neighbors! Two small ones, and always the big donut country. I attached a picture to my previous comment to make it more clear.
In your example the blue country could be yellow and that leaves the other yellow to be blue. Now no identical colors touch.
You still have two red countries touching each other, what are you talking about?
Oops I meant the red one goes blue.
Whoops I should’ve been clearer I meant two neighbours within the donut. So the inside ones could be 2 or 3 colours and then the donut is one of the other 2 or the 1 remaining colour.
You’re right. Bad example from my side. But imagine this scenario:
That map is actually still quite similar to the earlier example where all 4 donut hole countries are the same. Once again on the right is the adjacency graph for the countries where I’ve also used a dashed line to show the only difference in adjacency.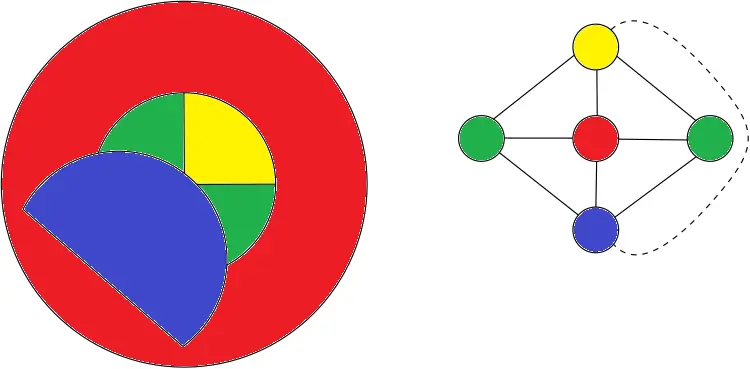
Oh wow, now I feel dumb. Thanks.
Feeling dumb is just the first step in learning something new
Make purple yellow and one of the reds purple.
…There is no purple though?