Since I have studied mesoamerican languages, which includes base 20 numbering systems, I was curious to see what may happen by following the same rules for 7 in decimal.
The following will be written as follows.
7*x : 5
Which implies any number that is divisible by 7 can be found by the following programmable formula (ignoring integer division) (y - y % 10) / 10 + (y % 10) * 5 where y = 7 * x (Erm, just watch this video).
Maya Number : Multiplier
7*x : 6
13*x : 2
17*x : 6
Just what I’ve seen so far…Am needing sleep, and am older and a lot more decrepit, so have no clue if I’ll ever work this out fully and completely in the future, heh. Meh, it was fun while it lasted…Time for sleep…
If anyone else wants to play around with it, I do have a few pari/gp functions written that can be used to work with it.
\\ Maya(x) convert a decimal number x into a Mayan number as a list.
Maya(x) = { V=List();while(x>0,listinsert(V,x%20,1);x=x\20);return(V) }
\\ Maya2Dec(X) convert a Maya number list X to a decimal number.
Maya2Dec(X) = { t=0;for(x=1,length(X),t=t*20+X[x]);return(t) }
g(x,t) = x\20+(x%20)*t;
Edit:
Since this was rather confusing, I’ll try a different method to explain this.
A base 20 system, such as the Maya or Nahuatl/Aztecs counted in, the single digits would be 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19, as they counted with both fingers and toes.
Another way to aid in this, in the Tzotzil Maya language, they count based on a person or persons.
20 = jtob
21 = jun scha’vinik (2nd person’s one [digit])
22 = chibal scha’vinik (2nd person’s two [digits])
39 = balunlajunebal scha’vinik (2nd person’s 19 [digits])
40 = cha’vinik ([the whole] 2nd person. Each person has 20 digits, so including the second person is 40 digits all together).
Now, with that, lets look over the 13\x : 2 that I wrote above.
Is the number 6875 divisible by 13? In a base 20, 6875 would be written as 17:3:15, using the colon to differentiate the digits from a base 10 system. Thus, 17 * 20^2 + 3 * 20 + 15 = 6875.
- 17:3 + 2 * 15 = 18:13 (Base 10 ; 343 + 30 = 373)
- 18 + 2 * 13 = 2:4 (Base 10 ; 18 + 26 = 44)
- 2 + 2 * 4 = 10 (No! This is not divisible by 13).
Is the number 7527 divisible by 13?
- 18:16 + 2 * 7 = 19:10 (Base 10 ; 376 + 14 = 390)
- 19 + 2 * 10 = 1:19 (Base 10 ; 19 + 20 = 39. Check, this is divisible by 13).
Hopefully that is better.
Edit 2:
And here is the work in Maya. (Using circles around the + and = signs to make it easier to read. Plus, using very well defined parentheses to differentiate between the line used for the digit spacer and as showing multiplication).
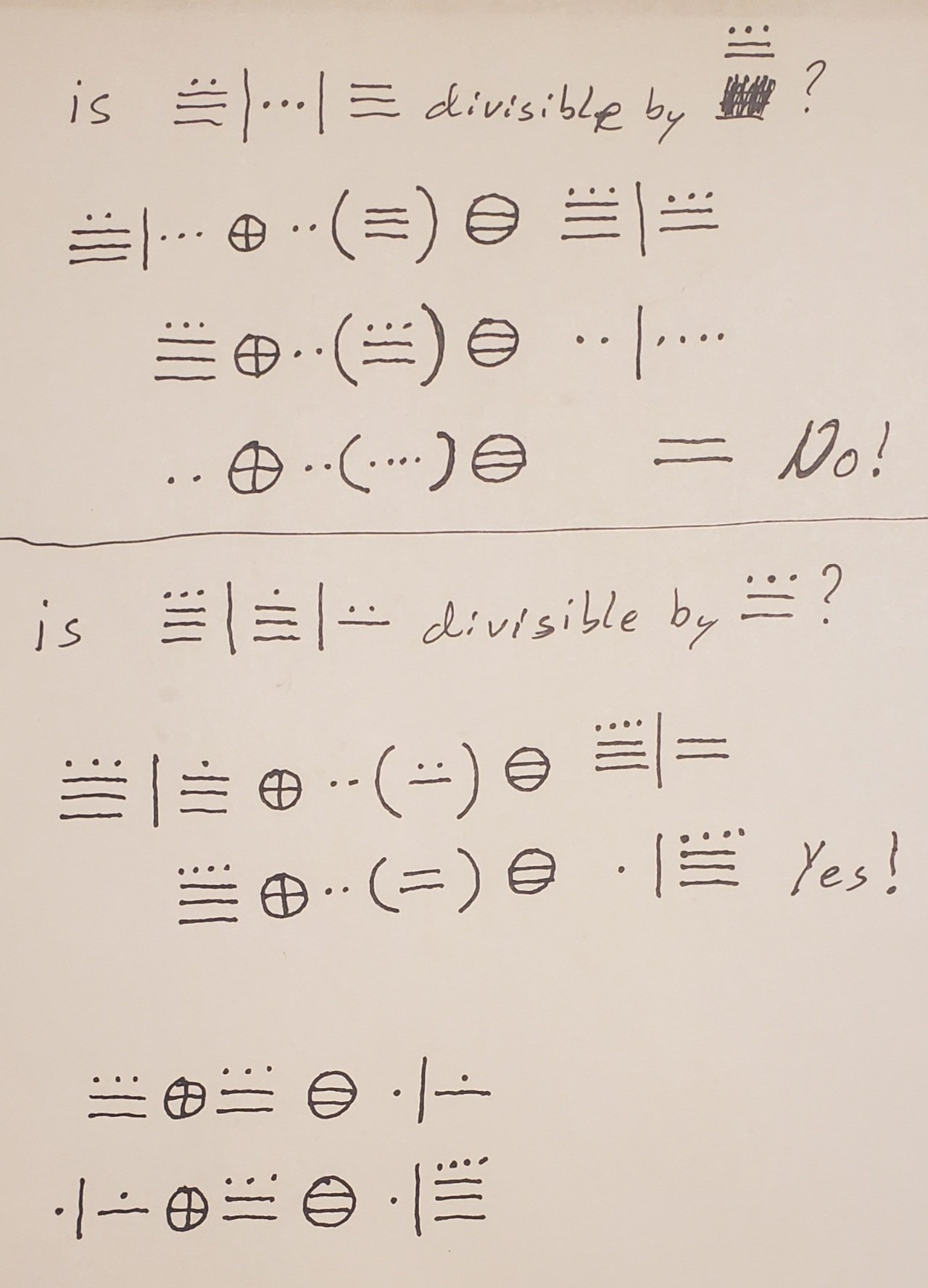
In simple English… A number is divisible by 7 if the difference between 2 times the last digit and the remaining digits is divisible by 7.
Examples:
- Is 14 divisible by 7? 4*2=8. 8-1=7. Check.
- Is 28 divisible by 7? 8*2=16. 16-2=14. Check.
- Is 182 divisible by 7? 2*2=4. 18-4=14. Check.
- Is 1323 divisible by 7? 3*2=6. 132-6=126.
- Is 126 divisible by 7? 6*2=12. 12-12=0. Check.
OP, if I have misunderstood your reasoning, please correct me.
This made the code so much clearer. Thanks for the explanation
Not sure, (“Older and a lot more decrepit” doesn’t mean “younger an a lot more mentally sound”, heh. Do wish I could change that, but meh, I can’t).
Anyway, I did find a method similar to what you wrote, so I can redefine it in your terms.
A base 20 number is divisible by 7 if the difference between 8 times the last digit and the remaining digits is divisible by 7.
Ok, a little description on a base 20 number (Think Mayan and Nahuatl/Aztec numbers). 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19 should be considered single digits. So a base 10 number, 7*17 = 119 (1*10^2+1*10+9), would be 7*17 = 5:19 in a base 20 system (5*20+19).
- is 1:8 divisible by 7? (28 in base 10). 8*8 = 3:4. 3:4-1 = 3:3
- is 3:3 divisible by 7? 8 * 3 = 1:4. 1:4 - 3 = 1:1 (1*20+1 = 21).
- is 9:2 divisible by 7? (182). 2*8 = 16. 16-9 = 7 Check.
I’ll just leave that there. So a long weird way of saying, yes, that’s pretty much my reasoning, but not exactly at the same time. As the first message included the base 20 numbers divisible by the base 20 single digits 7, 13, and 17. (Hopefully that came off a little better).
(Note: Saying “base 20 number[s]” is not important overall. Just being overly descriptive to differentiate between base 10 digits and base 20 digits).
- is 1:8 divisible by 7? (28 in base 10). 8*8 = 3:4. 3:4-1 = 3:3
One hell of a showerthought there mate.
That’s a baththought at this point.
Timmy, so help me god if you are doing math in there again!
How long are your showers?
I could spend the remainder of eternity at the bottom of Niagara falls and still not be able to grasp what he is saying.
Here is an alternative Piped link(s): https://piped.video/UDQjn_-pDSs
Piped is a privacy-respecting open-source alternative frontend to YouTube.
I’m open-source, check me out at GitHub.
I did find that it can be done arbitrarily. Mind is definitely not into writing about it, though, but here’s the gp code I wrote to look it over.
/* There may exist a 0<=t<s such that s divides both x and (x+(x%d)*(t*d-1))/d. To show this for solving for divisibility of 7 in any natural number x. g(35,5,10) = 28 g(28,5,10) = 42 g(42,5,10) = 14 g(14,5,10) = 21 g(21,5,10) = 7 */ g(x,t,d)=(x+(x%d)*(t*d-1))/d; /* Find_t( x = Any natural number that is divisible by s, s = The divisor the search is being done for, d = The modulus restriction ). Returns all possible t values. */ Find_t(x,s, d) = { V=List(); for(t=2,d-1, C = factor(g(x,t,d)); for(i=1,matsize(C)[1],if(C[i,1]==s, listput(V,t)))); return(V); }One thing that I noticed almost right away, regardless what d is, it seems to always work when s is prime, but not when s is composite.
Too tired…Pains too much…Have to stop…But still…interesting.
Huh, I don’t really need to check numbers for that but I’ve never heard of Pari/GP, so that was interesting.
Yeah, before my mind decided it didn’t like learning any more, I had learned the gist of Bell and Noll’s calc, then switched to gp a few years later…for which I can not remember why, but I can still remember how to use it fairly well.






