You have 20 apples that you put into 5 boxes. “How many apples per box?” 20/5=4. Easy.
You have 20 apples that you put into half a box. “How many apples per box?” 20/0.5=40. You can see how 20 apples in half of a box implies 40 apples per full box.
You have 20 apples that you don’t put into anything. “How many apples per box?” 20/0=? What box? What are you talking about? How can you suggest that there are a number of apples per box when there’s no box to begin with? Lunatic!
Mind === blown
Wouldn’t half a box just be 1 box that is half the size of a full-sized box?
Also, how can you fit twice as many apples into a box just because it’s a smaller volume? You still only have 20 apples. And if anything you wouldn’t be able to even fit that quantity probably since it’s a smaller volume. Right?
deleted by creator
The key is understanding how divisions between 0 and 1 work. Say you take 2/0.5, you end up with 4. 2/0.25 you end up with 8. As you can see, those numbers get big fast. 1/0.0001 is 10,000.
As you approach 0, you get increasingly large numbers. If you flip it negative, again as you approach -0, you have increasingly big negative numbers. As you approach 0 from both sides, you approach positive and negative infinity. But what goes in the middle, at exactly zero? We don’t know, There’s no sensible value there, so it’s considered to be undefined.
In computers, it’s usually either an error, or represented with NaN (Not a Number) when you want to avoid throwing an error condition. NaN is defined so that any operations involving NaN is also NaN, so your entire equation becomes NaN.
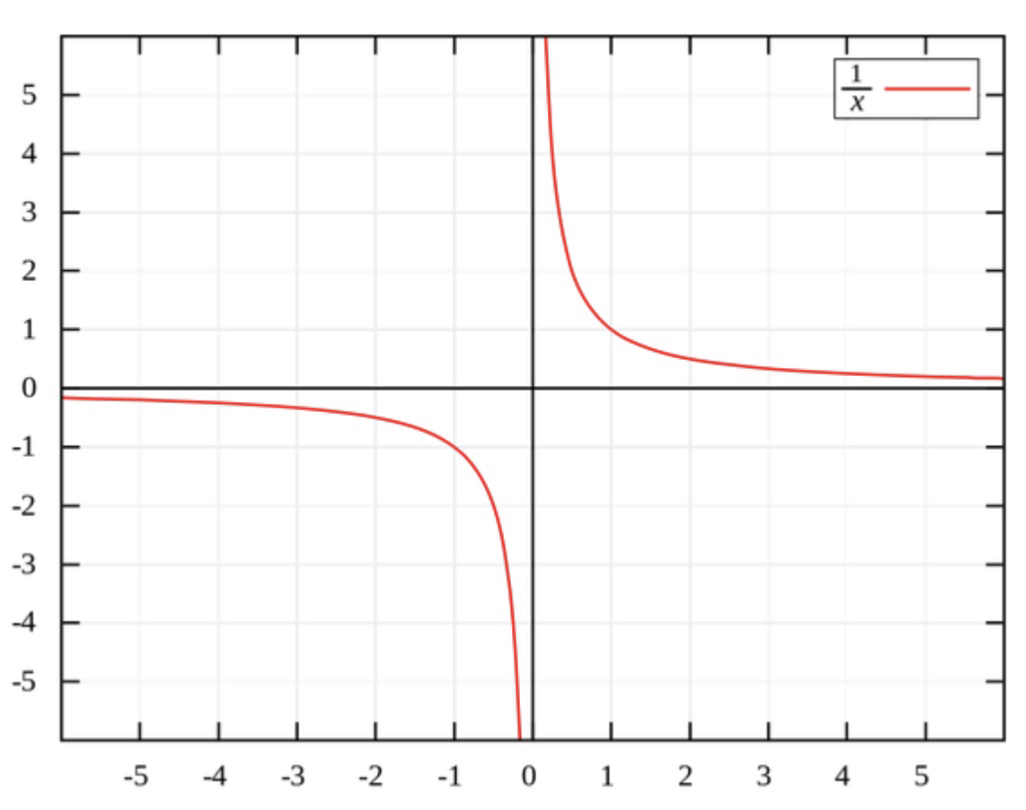
Easiest way to visualize that is to input
y = 1/xin a graph calculator (Desmos is nice). You clearly see it going to negative infinity then back at positive infinity.With some other operations like negative square roots, we’ve made up the imaginary number i, which is defined to be the square root of -1, and we can make it do useful things. But what can we reasonably do with the result of dividing by zero? It behaves like infinities: you can’t really add or multiply them, or divide them. You’re just stuck with it. It’s impossible to represent, it’s Not a Number.
And an important note about imaginary numbers is there more of a band aid solution because we chose to lose information when doing positive exponentials, when in reality both positive and negative answers are equally valid mathematically (though sometimes not physically).
So math doesn’t care about our conventions and sometimes we need that information back, hence complex numbers.
Multiplying anything times 0 = 0 though doesn’t just have 2 possible outcomes, it has infinite for the variable multiplied. With such aggressive information loss its usually hard to retain any realistic information, though it is possible with proper limits
It is undefined because the inverse of division is multiplication. If you multiply by zero, every answer is zero. If you try to invert that operation you can’t know which number was multiplied by zero to get zero because multiplying by zero doesn’t produce a unique answer for each operation.
Additionally, if you take the limit of 1/x as x approaches zero from the positive side the result approaches positive infinity. If you take the limit from the negative side it approaches negative infinity.
An interesting thing to think about is whether multiplication by zero really makes much sense in the concrete world. You can’t really have zero groups of something or some number of groups of zero. Zero groups of anything is still nothing. We can think of that abstractly once we have the abstract concept of numbers, but in the real world that idea is nonsense.
You mean that it’s undefined?
You can think of a cake. You can divide a cake into 4 pieces or 2 pieces or basically not divide it, by ‘dividing’ it into 1 piece.
But it’s not possible to divide a cake into 0 pieces. It doesn’t make logical sense. You have to eat it (subtract from it) to actually make 0 pieces. With division, the sum of all pieces has to be 1 cake. If there’s one cake, there’s at least one piece.
What’s confusing is that we have separately decided that ‘dividing’ a cake into 0.5 pieces means you multiply it by 2. So, either 2 cakes or a cake that’s twice as large. That is why some mathematicians do treat 1/0 as ∞.
Its kinda interesting to me that math needs to fall back on the realm of language to express rhat which cannot be mathematically modelled, despite the fact that the structural format of the question inherently and one would conclude is more the question of numbers rather than words that undefined is inclusive of
Like, it makes total sense on an intuitive level and with a little rhetoric but it seems a little strange that on such a mathy issue, we need language (beyond the letters that algebra nominally requires) full-stop to express even what amounts to a non or undefined which is seemingly a more linguistic construct.
I mean, math really is just language. That’s why people argue over PEMDAS vs BODMAS and we have all those memes about “what’s the right answer to this arithmetic calculation?”
It just so happens that the math language we use is sufficiently refined to very closely reflect how things work in non-conceptual space (ie the Real World), often so much so that we can use it to get a new protective on that non-conceptual space and get insights about it that we didn’t have before.
Math and language are really both just symbols we use to describe the Real World; they’re basically the same thing.
I think you are really touching on math philosophy here. Is math discovered or invented?
Just because you can WRITE x/0 doesn’t mean you should be able to perform the operation. Because it’s conversion to language is non sensical (to you, at this moment) does heavily imply The operation is meaning or arcane.
You asked for a simple explanation of the math, so people analogized it into common language. That doesn’t necessarily mean the common language provided is a perfect mapping. The best answer for a math question will always be a math answer.
I think I’m all set, math pun intended and also I really appreciate your critique here 📐
Edit: i like that you brought up mapping since maps are in a similar sense only ever capable of representing something where distortion is inevitable even though irs fundamentally workable for the intended purpose
There are some good answers here already. I feel the need to add something, though.
If I gave you a number, 6, and multiplied it by 2 you’d get 12. If I asked you to “undo” the multiplication, you’d divide it by 2. So, you can think of division as the “inverse” of multiplication.
So: 12 * 1/2 = 6.
6, when doubled is 12, and 12, when halved, is 6. You can never double 6 and get 14. We say that multiplication between two (nonzero) numbers has a one-to-one relationship.
Then, let’s say I asked you what 0*6 is. And you’d say 0*6=0.
Then, let’s say I didn’t know what we started with. I give you this equation and ask you to find a value for x:
0*x=0
What is x? X can be anything here, 1, 17, pi, all numbers work. You can even choose 0.
Could you try 0*x*1/0=? How would you choose one number to be correct?
There is no “undo” button here. 1/0 is meaningless because we can’t assign it a unique value. A math person would say, “0 has no multiplicative inverse”.
Is it fair to suggest or infer that in order for division to be possible, the divisor must be partitive of the dividend? Like 6 can never be partitive of 14 in the whole number sense such that axiomatically 14/6 = undefined in some vague sense that I can be damned to elaborate or defend currently?
I can’t parse this paragraph.
14/6 has a solution, its 2.3333……
Multiply 14/6 by 6 and you get 14 again. You can always go back to the initial state when you know what actions are taken, unless you’ve multiplied by 0.
Like 6 can never be partitive of 14 in the whole number sense such that axiomatically 14/6 = undefined in some vague sense that I can be damned to elaborate or defend currently?
If I am understanding what you’re trying to say, then yes, 14/6 does not have a solution in the sets of natural numbers, whole numbers (natural numbers and zero), and integers (whole numbers and the negative numbers). This is because 14 is not a multiple of 6.
However it does have a solution in the set of rational numbers and by extension, the real numbers. Thus, if we’re talking about real numbers, 14/6 does have a solution: 2.3̅3 (two point three three repeating).
I recognize that I’m veering very closely, if not already have gone to explaining this in axiomatic terms. I apologize.
At any rate, if you’re wondering if there is any similar extensions to the real numbers that can accommodate 1/0, as far as I understand, such extensions, if they do exist in the way you want them to behave, would still run into the same problems other replies to your post have described. Because of those difficulties (among others), in the two extensions I’ve looked at (hyperreals and the surreals), division by zero (and thus, 1/0) is still impossible in general, but are allowable in certain circumstances corresponding to the situations where y/x at the limit as x→0 exists or is +infinity or -infinity (but not both). However, as far as I understand it, in the real projective line, where there is a “point at infinity” added, you can define 1/0 as being that point at infinity.
EDIT: added some important clarification.
You have nothing to apologize for, this is a very eclectic discussion from the get-go ♾️
Thanks! I hope my reply has helped you somehow. I think that “point at infinity” concept from the real projective line (which I added as an edit) is the closest to a “solution” to your question. It’s likely not an end-all-be-all solution to 1/0 though, since, as far as I understand it, it “collapses” -infinity and +infinity to just one point at infinity, which might not be a desired property in certain circumstances.
I so wish I had taken like advanced maths + calculus and not had a narcissistic tormenter of a parent so I could actually think and digest math. None of the above “equation” would have been possible and I mourn that fact but I hope to incrementally refine my thinking and possibly approach that level over time if I can by diffusion like in this thread (a little bit)
It is possible to grasp (relatively) advanced math like in this discussion via self-study. I myself came from a different background (engineering) though I’ve been somehow interested in math since high school. I wish I can recommend some material for studying such fields of math from a non-math background (at least at the start) but maybe that should be saved for a separate thread. I do remember encountering such a thread in the other place, but it won’t hurt much to ask for it here (if there isn’t already such a thread here).
This clicked for me when my teacher explained it in terms of slopes.
The video here breaks it down nicely. https://virtualnerd.com/sat-math/geometry/slope/infinite-slope-definition.
So you have a vertical line with an infinite slope. There are no changes in x as you traverse the line, only changes in y. Or said differently, the line is described entirely by a single x-value which corresponds to every possible y-value.
If you think of it in terms of a function, it’s extremely problematic because you no longer have a mapping of a single y-value to each x-value. This violates the requirements of a function. It’s not possible to define the slope value when rise/run is something/zero, therefore we describe the function value as “undefined”.
But even though we can’t calculate a slope or address it with a function, it’s pretty easy to visualize and understand a vertical line. So that’s what dividing by zero represents in concrete terms.
I am surprised that nobody pointed out that there is a mathematical structure where you can divide by zero, the wheel:
Kinda wonder how a sphere of all things can possibly be modelled? I even heard you can like cut a sphere in half and axiomatically retain or conserve the prexisting volume or something to that effect. Like you could tangibly split it in two and conceptually still have >= prexisting volume or something? It seems absurd but I’m sure someone can hand-wave or radically justify exactly that somehow
There’s a veritasium or vsauce video on that.
Can you link to that? I have zero idea how to intelligibly find a result to this inline with what you’re suggesting
I believe it is the Vsauce video titled The Banach-Tarski Paradox.
Thank you so much for naming this seemingly crazy conjecture for me. Heard about it so vaguely forever ago and it seemed nuts but nice to finally to more (in)formally get to investigate it
Trying to interpret math in non-abstract terms is often misleading and just creates confusion. a/b is a solution to the equation bx = a, nothing more, nothing less. Then maybe you can use it to model a real-life situation, maybe not.
Okay I’m not a mathologist - in fact I hate the guy - so here’s how I see it. If you have one apple, and you divide it zero times, you still have one apple. That’s it.
If I have 6 apples and I hand them out among 3 people, each person has 2 apples. All the people together have 6 apples, and I have none.
If I have 6 apples and I hand them out among 12 people, each person has 1/2 apples. All together, they have 6 apples, and I have none.
If I have 6 apples and I try to “hand them out” among 0 people, I have nobody to give any apples. I still have all 6 apples, and “all” the “other people” have none. All together, they have 0 apples, and I still have 6.
Since I can’t “hand them out”, I can’t divide them. That “division” is impossible to perform.
If you divide it zero times you have an apple. The discussion is about dividing by zero.
You can cut something into 2 pieces, or 1 piece, but you can’t cut something into 0 pieces.
deleted by creator
This makes me think… if we consider dividing as an action, even when dividing by one you are still using a cutting action, you just miss the apple. But with dividing by 0, it’s one less cutting action… so there are 0 cutting actions. Then if you divide by -1, you’re removing one hypothetical cutting action, ie removing the action of missing the apple. So, 10 / -2 should really equal 20, because you’re reversing a cutting action that caused the total to be cut in half and equal 10…
Explain what exactly?
You can divide 2 apples between two people, or between four people, but you can’t divide them between zero people. That premise doesn’t make sense, the question is incomplete to be answerable.
By expanding our scale with another dimension (complex numbers in math) we expand the question. How do we add another dimension to the physical, practical anecdote? 🤔
Can you explain negative multiplication is in this sense? Like
-1 * -1to make it simple?Edit: is it like
the enemy of my enemy is my friendtype deal?Yes, exactly. A double negation.
The opposite of the opposite is the same again.
/edit: anecdotes and simplification are often a balancing act between between simplicity and (thorough) correctness. The opposite thing and enemy of enemy (in a two party premise) fit and practically correct for the Negation of the multiplication. It doesn’t thoroughly represent the multiplication part. But I think the negation is what you were looking for?
Dividing by zero is undefined in the realm of real numbers and basic arithmetic because there’s no meaningful answer. It’s not an abstract concept; it’s simply mathematically impossible due to the nature of division.
I guess if I were to spill over to the non-numerical and semantical or more linguistically axiomstic representation here,:
- The divisor is a number (1)
- The dividend is a number (0)
- A number divided by another number consequently produces another number
- Does mathematics line up with CS on the whole NaN designation? I might be conflating fields or… I dunno. I’m sure there’s a palpable issue here you guys can lead this ass to override whatevers going on in my head
Your third axiom is faulty.
Divisor, Dividend, Quotient. If your axiom is correct, then when I give you any two of these numbers, you should be able to give me the third. Yet when I give you an arbitrary quotient, and a divisor of 0, there is no dividend you can give me to complete the set.
I can thus give you an infinite number of exceptions to your axiom.










