Guaranteed to sort the list in nearly instantaneous time and with absolutely no downsides that are capable of objecting.

The creation and destruction of universes is left as an exercise to the reader

Instead of destroying the universe, can we destroy prior, failed shuffle/check iterations to retain o(1)? Then we wouldn’t have to reload all of creation into RAM.

What library are you using for that?

Since randomizing the list increases entropy, it could theoretically make your cpu cooler just before it destroys the universe.

you should post this on lemmy.ml

deleted by creator

// portability

Gave me the giggles. I’ve helped maintain systems where this portable solution would have left everyone better off.

I wonder how many 2 item lists have been sorted that way IRL.

Camelcase in python, ew, a fundamentalist would do that

Where’s this yhwh library, can I install it with pip? Seems like it could have potential for some of my projects.

New templeOS fork?

yhwh looking suspiciously like an LLM

Those bitflips are probably more likely to skip the section erroneously than waiting for the array to be sorted.

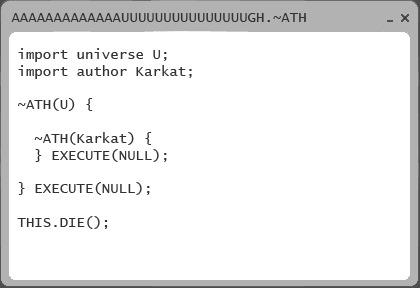
Reminds me of a program in Homestuck. It’s code that iterates until the author/universe dies, then executes some unknown code. The coding language is ~ath, or TilDeath.

Not necessarily. I don’t have the numbers in front if me, but there is actually a probability that, past that point, something is so unlikely that you can consider it to be impossible (I.e. will never happen within the lifetime of the universe)

I’m not sure there’s any guarantee that it will ever be sorted, since bit flips will be random and are just as likely to put it more out of order than more in order. Plus if there’s any error correction going on, it can cancel out bit flips entirely until up to a certain threshold.

Though I’m not sure if ECC (and other methods) write the corrected value back to memory or just correct the signals going to the core, so it’s possible they could still add up over time and overcome the second objection.

Bogosort is great! Also easy to implement

Everyone does… it’s funny how it eventually works.

I hear, it actually significantly increases the chance of the miracle occurring when you pass the array into multiple threads. It’s a very mysterious algorithm.

It would actually have happened an infinite amount of times already, if either the universe is infinite, or there are infinite universes.

Goos stuff, I will start using it. My code needs to chill out anyway

I don’t think you can check if array of n elements is sorted in O(1), if you skip the check though and just assume it is sorted now (have faith), then the time would be constant, depending on how long you’re willing to wait until the miracle happens. As long as MTM (Mean Time to Miracle) is constant, the faithfull miracle sort has O(1) time complexity, even if MTM is infinite. Faithless miracle sort has at best the complexity of the algorithm that checks if the array is sorted.

Technically you can to down to O(0) if you assume all array are always sorted.

Skiena’s Algorithm design manual is very widely recommended for learning algorithms, I’ve also heard good things about A common sense guide to algorithms and data structures. Skiena’s also has video lectures on YouTube if you prefer videos.

From what I’ve seen, a common sense guide seems to be more geared towards newer programmers while Skiena assumes more experience. Consequently, Skiena goes into more depth while A common sense guide seems to be more focused on what you specifically asked for. algorithm design manual

A common sense guide

don’t get discouraged. sorting algorithms occur frequently in interviews, and yes you use them a decent amount (especially in languages without built in sorts like c) but they are one of the harder things to visualize in terms of how they work. I’d say avoid anything recursive for now until you can get selection and insertion down pat. check out geeksforgeeks articles on them, but also don’t be afraid to Google willy nilly, you’ll find the resource that makes it click eventually.

in terms of efficiency, it does become a little more difficult to grasp without some math background. big o is known as asymptomatic notation, and describes how a function grows. for example, if you graph f1(x)=15log(x) and f2(x)=x, you’ll notice that if x is bigger than 19, then f2(x) always has a higher output value than f1(x). in computer science terms, we’d say f1 is O(log(n)), meaning it has logarithmic growth, and f2 is O(n), or linear growth. the formal definition of big o is that f(x) is O(g(x)), if and only if (sometimes abbreviated as iff) there exists constants N and C such that |f(x)| <= C|g(x)| for all x>N. in our example, we can say that C = 1, and N>19, so that fulfills definition as |15log(x)| <= 1|x| whenever x>19. therefore, f1(x) is O(f2(x)). apologies for just throwing numbers at you, (or if you’ve heard all this before) but having even just the most basic grasp of the math is gonna help a lot. again, in terms of best resources, geeksforgeeks is always great and googling can help you find thousands of more resources. trust that you are not the first person to have trouble with these and most people before you have asked online about it as well.

I also highly reccomend grabbing a copy of discrete mathematics and it’s applications by Kenneth Rosen to dig farther into the math. there’s a few other types of asymptomatic notation such os big omega and big theta, even little o, that I didn’t mention here but are useful for comparing functions in slightly different ways. it’s a big book but it starts at the bottom and is generally pretty well written and well laid out.

feel free to dm me if you have questions, I’m always down to talk math and comp sci.

edit: in our example, we could also pick c =19 and n = 1, or probably a few other combinations as well. as long as it fills the definition it’s correct.

On a long enough time scale, yes, it will get tidy.